Using comparative judgement to assess mathematical reasoning
This post is part of a series outlining No More Marking’s initial findings from a mathematics research project, carried out jointly with Axiom Maths, in 2023-2024. You can find the previous post on the multiple-choice assessment here.
As part of the project, Year 7 students took part in a comparative judgement assessment of mathematical reasoning skills using the No More Marking platform. In the assessment, students were asked to answer two questions:
Question A
The digits of the 3-digit whole number 384 add up to 3 + 8 + 4 = 15.
How many different 3-digit whole numbers can you find whose digits add up to 24?
Question B
Ari has a pile of cookies and a pile of boxes.
When he puts seven cookies in each box, he has one empty box left over.
When he puts six cookies in each box, he uses all the boxes but has one cookie left over.
How many cookies did Ari have?
The questions were deliberately designed to be quite open, and students were instructed to “be as thorough as you can with your answer and explain how you tackled the problem as much as you can. It is fine for you to draw pictures if you want.” The aim of the assessment was to try and measure students’ mathematical understanding and problem-solving skills. Once completed, teachers from the schools involved judged the student answers using the NMM platform.
In total 1776 students from 17 schools completed the comparative judgement assessment. 142 teachers from the schools completed 16840 decisions, therefore 9.5 decisions per student. This is close to NMM’s recommendation of 10 judgements per student.
After the completion of the judging, examples of student responses at each scaled score of 20, 40, 60, 80 and 100 were chosen and examined to try and see the progression in the students’ problem-solving skills.
For this piece, the student did identify some numbers that added up to 24 but not single digits. On the second question some diagrams were used although there is no clarity in how they are being used.
For this piece, there is the beginning of some understanding of one of the problems, but no clear evidence of any understanding for the other.
Here, some understanding is shown for both problems, although still not approaching fully correct answers. Some evidence of a systematic approach is shown for the second question in terms of the table.
Here, the student is approaching fully correct answers. The systematic approach that is used is not quite as clear as the answer below.
Once again, the student is approaching fully correct answers. However, there is greater evidence of a systematic approach to using the combinations of 7, 8, and 9, and the use of the table in the second question.
Looking at the general progression in student responses, there does seem to be a progression from showing no clear understanding of how to approach the problem, to showing some understanding and starting to develop a possible systematic approach, through to approaching fully correct answers and being clear with systematic approaches to the problems. One of the advantages of comparative judgement is that the scoring of the answers is not just about correct or incorrect answers, but also starting to gain some insight into how and whether the students could approach the mathematical reasoning tasks.
In the next post we will examine the relationship between the above comparative judgement scores and the scores achieved on the multiple-choice assessment in the project.





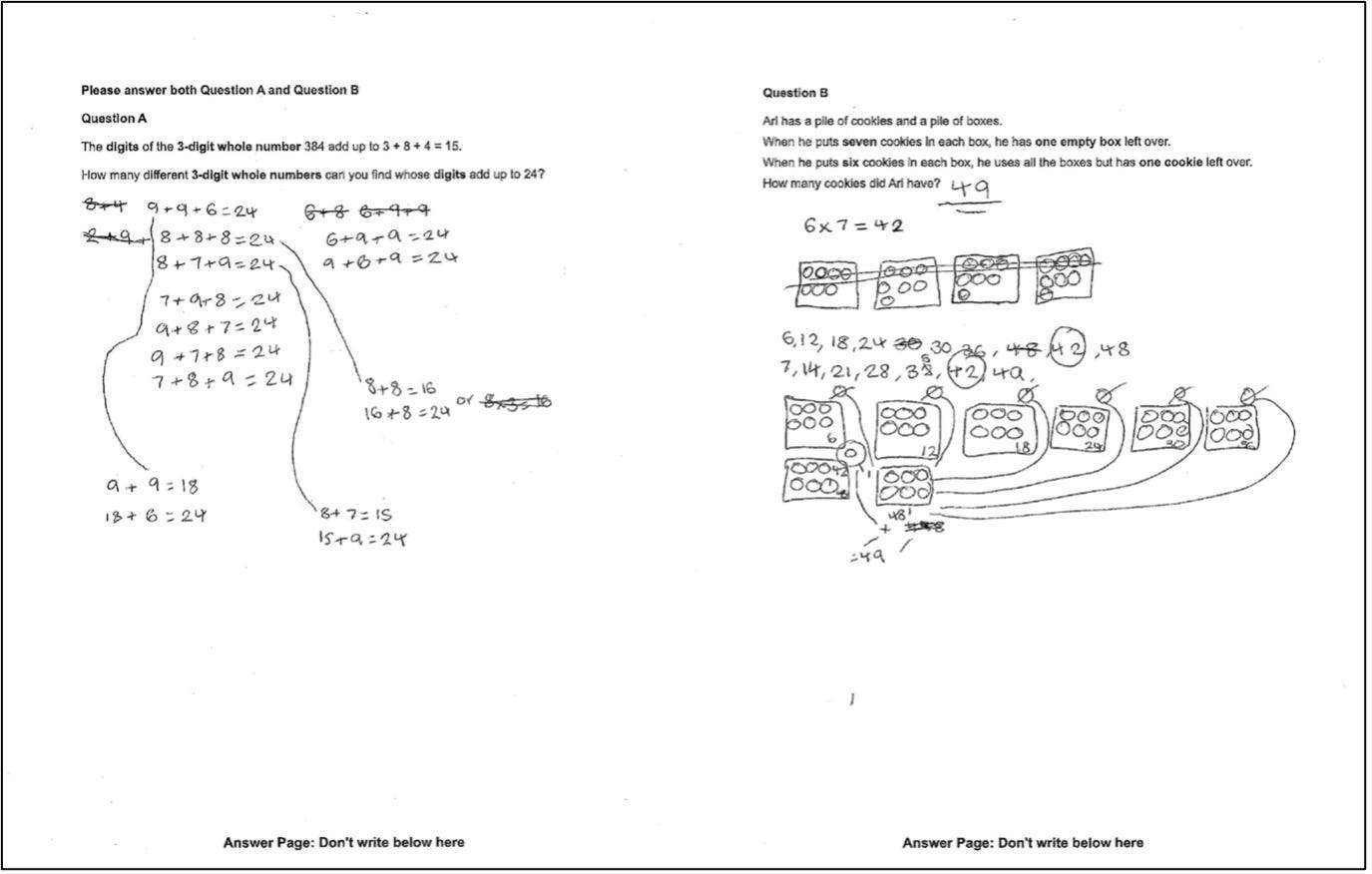

"Once again, the student is approaching fully correct answers, although technically, the first question is not quite correct (some of the examples, e.g. 9 + 9 + 6, did not use different single digits)."
This just seems flat-out wrong to me. The original problem statement did not require the digits to be different; instead, it only required that the 3-digit numbers are distinct:
"The digits of the 3-digit whole number 384 add up to 3 + 8 + 4 = 15. How many different 3-digit whole numbers can you find whose digits add up to 24?"
So 9 + 9 + 6 is in fact a perfectly valid solution to this problem.