Why crossings-out are important in solving mathematical problems

This post is part of a series outlining No More Marking’s initial findings from a mathematics research project, carried out jointly with Axiom Maths, in 2023-2024. You can see our first post on the multiple choice assessment here. The second post on the comparative judgement assessment is here. And the third post on comparing the multiple choice with the comparative judgement is here.

As part of the project, Year 7 students (in England so aged 11 to 12 years) took part in a comparative judgement assessment of mathematical reasoning skills using the No More Marking platform. In the assessment, students were asked to answer two questions. In this analysis, we focus on the first question:

The digits of the 3-digit whole number 384 add up to 3 + 8 + 4 = 15.

How many different 3-digit whole numbers can you find whose digits add up to 24?

In the comparative judgement, the work of 362 students were moderated by the participating schools. Their answers were scored on a 0 to 100 scale. Following the judging, we looked at the students’ answers in order of lowest to highest scores to see if we could see a progression in approaches to the problem. One simple element that we noticed was whether students crossed out any of their work during their answering process. Therefore we decided to explore this a little deeper.

Analysing the crossing-outs

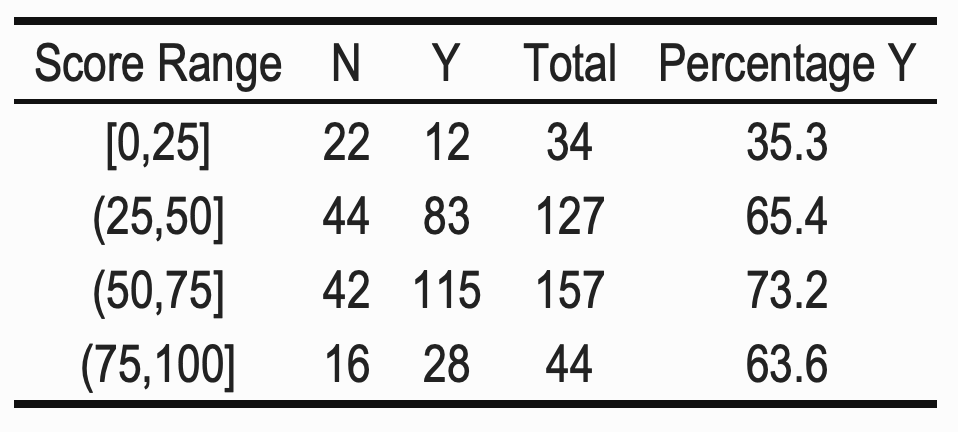
The student answers were assigned a Y or N code depending on whether any crossings-out were observed or not. We then looked at the the percentages of Ys and Ns in the scale score ranges 0-25, over 25 to 50, over 50 to 75, and over 75 to 100.

Plotting the percentage of crossed-outs with scaled score range:

We can see that there is an increase in the crossing-outs over the initial score ranges and then a fall at the end. Is this change significant? We carried out a two-way Chi-square test on the data in Table 1 and found that the percentages did change significantly over the score range groups (Chi-squared = 18.02, df = 3, p-value < 0.01). Therefore, we found that there was a significant change in whether crossings-out were used across the scaled score ranges.

Why might this be?

Firstly, a straightforward reason might simply be that students wrote more as they moved up the scaled scores. But that doesn’t explain the dip at the highest score range. We think crossings-out have greater importance than that. Let’s have a look at one example answer.

Figure 2: Example of the use of crossings-out

There are a number of elements here in this answer. Firstly, a very exploratory stage where the student ‘played’ with 24 and simply divided by 4. This may or may not have informed their next attempt, but they crossed this division out, and used 6 in the combination of 698. But when they added these, they found that they did not add to 24 so crossed out 698. That perhaps informed their listing of numbers on the right-hand side. There are crossings-out there too (maybe 8+8+8 was their first attempt even before the division) and they crossed out 996 maybe because it was a repeat from above. They still haven’t got the wholly correct answer but you can see their process of trying things, crossing out, but using their attempts for the next stage.

And that is why we argue that crossings-out, or failed attempts, are important in solving mathematical problems (or any problems for that matter). A problem is a problem if the route to the solution is not immediately obvious. If it is obvious, it becomes a routine process. So whether it is a problem or not depends on the background knowledge and understanding of those tackling it. That might explain the dip in crossings-out for those achieving the highest scores. They were pretty confident about what they needed to do! It might also be why the lower scoring students had less crossings-out - they did not know how to approach the problem so did not explore very much.

The take-home message then in tackling mathematical problems - try something, doesn’t matter if it is obviously wrong, but use the information you get from your attempt to refine what you do. It doesn’t matter if you cross things out - in fact, if you are a student, your teacher might think that is a really good thing!